現在価値(PV)とは?
今回は、『現在価値』について、お話します。
いま、目の前にある100万円と遠い将来の100万円では、価値が違うということは直感的に理解できるでしょう。500年後に1億円もらえるとしても、今の私たちにとっては、1億円もの価値はありません。
むしろ、いますぐ、100万円もらった方がいい!、という人もいるかも知れません。このようにお金の価値は、未来になればなるほど小さくなっていきます。
具体的に考えてみましょう。
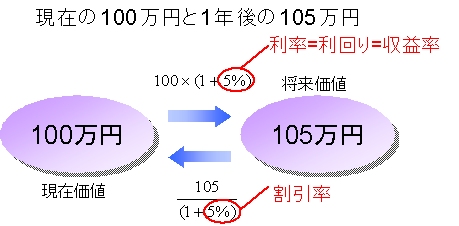
年利5%とすると、今日の100万円は、一年後には、105万円になっています。一年後でくらべてみると今日の100万円の方が来年の100万円よりも5万円価値が大きいことになります。この差をお金の時間価値といいます。
キャッシュを受け取る場合は、できるだけ早く受け取ったほうがその分、利息を稼げるからお得なのです。
一方で、キャッシュを支払う場合は、できるだけ遅くした方が有利というわけです。
このようにお金には時間価値があることから、時間軸が異なるキャッシュを比較する場合は、時間の価値を調整してやる必要あります。
将来のキャッシュが、現在のいくらに相当するかを計算するためには、利率で割り引くことで計算することができます。
先ほどの例でいえば、いまの100万円に1.05をかけて、一年後の価値は、105万円と計算することができました。このとき、105万円は、将来価値といいました。
一年後の105万円の現在の価値を求めるのは、この計算の逆を行なうわけです。
つまり、105万円を1.05で割ることによって、100万円と計算するのです。
あなたが行なったのこの計算プロセスを「一年後のキャッシュを金利で現在の価値に割り引く」といいます。
このように、将来価値から現在価値に換算するときに使う利率を割引率といいます。
現在価値から将来価値を求めるときは、割引率という言い方はしません。
利率、あるいは、利回り、収益率という言い方をします。ここが、混乱しやすい点です。
そうはいっても、将来価値と現在価値を換算するレートの表現の仕方が違うだけで、将来価値と現在価値は、まさに表裏一体の関係になっています。
この将来価値、現在価値、割引率はファイナンスでも、もっとも重要な概念です。
いや、むしろこれが理解できなければ、ファイナンスは先に進まないともいえるものです。しっかりと理解してください。
もう一度、三者の関係を復習しておきましょう。
現在価値に(1 + 利率)をかけると、将来価値になります。
将来価値を(1 + 割引率)で割ると、現在価値が求められます。
もちろん、ここでは、利率=割引率です。
5年先のお金を現在価値に割り引くという話になると、
(1 + 割引率)が(1 + 割引率)^5に変わることに注意してください。
現在価値の考え方をマスターすると、世の中のさまざま金融商品の理論価格を計算することができるようになります。
なぜなら、金融商品の理論価格とは、その商品が将来生み出すキャッシュフローの現在価値の合計だからです。
ついでに、永久債と呼ばれる債券の現在価値の計算方法を学習しましょう。永久債とは、過去に英国政府が発行した債券で、元本の償還はないものの、毎年一定額の利子を払いつづけるというものです。
こんな債券をあなただったら、いくらで買いますか。
永久債の現在価値を求めてみましょう。
毎年のキャッシュフローをC、割引率をrとすると、毎年永久にCを受け取れる永久債の現在価値
![]() は、
は、
| … |
と表せます。
両辺に
![]() をかけたものから、元の式を引いてみましょう。
をかけたものから、元の式を引いてみましょう。
| … |
| … |
![]()
![]()
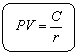
となることがわかります。
案外、簡単な式で求めることができるんで、びっくりですよね。
たとえば、毎年100万円を永久に支払い続けるという債券の
現在価値は割引率を5%とすれば、
| 万円 |
と求めることができるというわけです。
それでは、
毎年着実にキャッシュフローCが一定の割合gで、
永久に成長し続ける場合はどうなるでしょうか。
割引率をrとすると、
この金融商品の現在価値
![]() は、
は、
| … |
| 両辺に | をかけたものから、元の式を引くと、 |
| … |
| … |
![]()
| → |
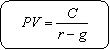
と求まるわけです。
これまた、結果的に、簡単な式になりました。
たとえば、
キャッシュフローが毎年3%ずつ成長する債券の現在価値は、
割引率を5%、
初年度のキャッシュフローを100万円とすれば、
| 万円 |
と求めることができるというわけです。
なんで、こんな小難しいことをやるんだ!
という感じですが、これらの考え方は、
企業価値を評価するときに大切となってきます。
今日のおさえていただきたい点は、
現在価値の考え方、
それに永久債・成長型永久債の現在価値の求め方です。